
Accepted at the International Conference on Machine Learning (ICML) 2025

pip install autoelicit
In this work we present a method for using large language models to elicit expert priors for linear predictive models and demonstrate how human experts can aid the process. We then compare these posterior predictions with those made through in-context learning, where language models make predictions directly. For this comparison, we estimate the in-context prior and posterior distributions and use the Bayes factor for model selection.
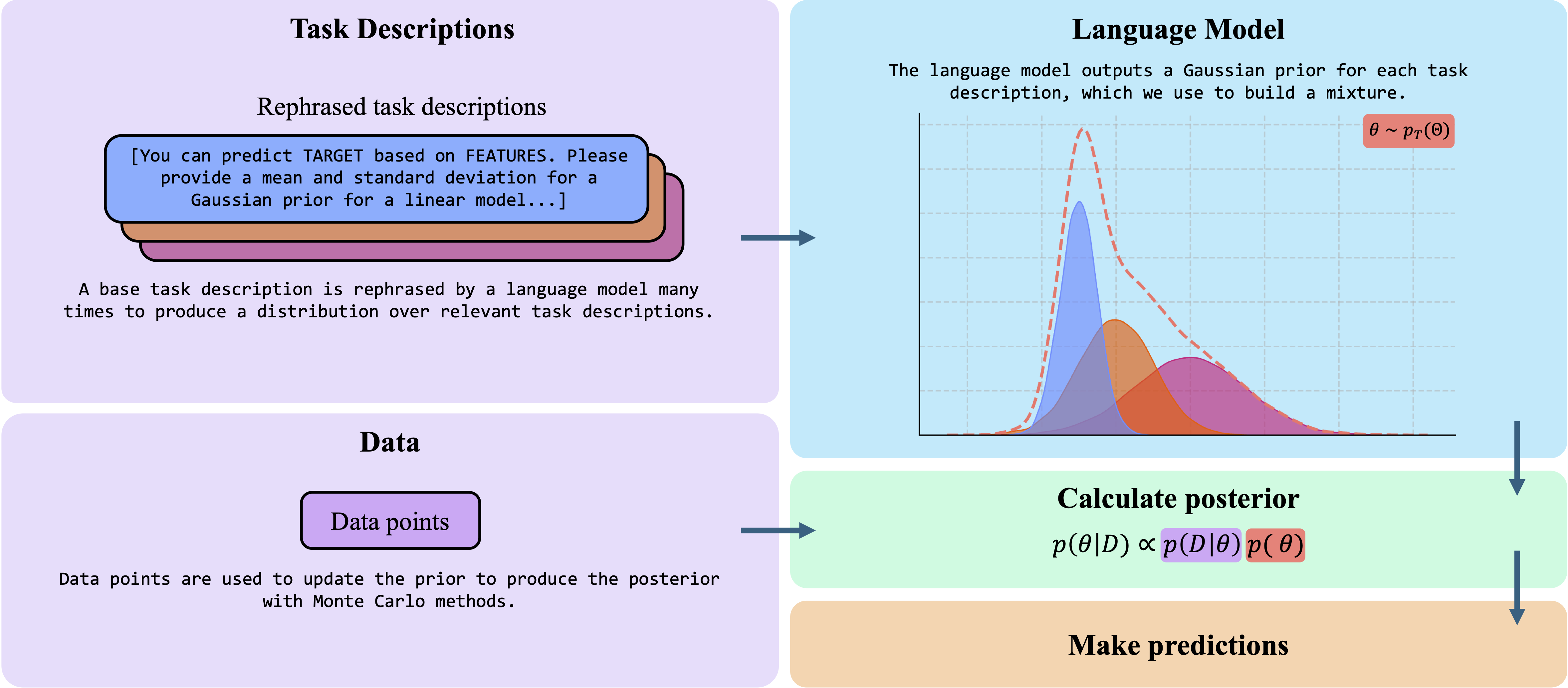
Large language models (LLMs) acquire a breadth of information across various domains. However, their computational complexity, cost, and lack of transparency often hinder their direct application for predictive tasks where privacy and interpretability are paramount. In fields such as healthcare, biology, and finance, specialised and interpretable linear models still hold considerable value. In such domains, labelled data may be scarce or expensive to obtain. Well-specified prior distributions over model parameters can reduce the sample complexity of learning through Bayesian inference; however, eliciting expert priors can be time-consuming. We therefore introduce AutoElicit to extract knowledge from LLMs and construct priors for predictive models. We show these priors are informative and can be refined using natural language. We perform a careful study contrasting AutoElicit with in-context learning and demonstrate how to perform model selection between the two methods. We find that AutoElicit yields priors that can substantially reduce error over uninformative priors, using fewer labels, and consistently outperform in-context learning. We show that AutoElicit saves over 6 months of labelling effort when building a new predictive model for urinary tract infections from sensor recordings of people living with dementia.
For a given task, we write a single user role and system role. We can then ask a language model to rephrase these roles \( k \) times each. By taking the product of these roles to form each prompt, we create \( k^2 \) unique task descriptions that define the problem setting. These task descriptions should all convey the same instruction and so allow us to capture some of the language model's variation to the way we specify the task.
As a synthetic example, we ask the language model to provide a prior distribution over the parameters of a linear model trying to make predictions on the following generated dataset: \[ y = 2x_1 - x_2 + x_3 \] where \( x_1, x_2, x_3 \) are the features and \( y \) is the target and \( X \sim N(0,1) \).
System role: You're a linear regression predictor, estimating the target based on some input features. The known relationship is: 'target' = 2 * 'feature 0' - 1 * 'feature 1' + 1 * 'feature 2'. Use this to predict the target value.
User role: I am a data scientist working with a dataset for a prediction task using feature values to predict a target. I would like to apply your model to predict the target for my samples. My dataset consists of these features: ['feature 0', 'feature 1', 'feature 2']. All the values have been standardized using z-scores. The known relationship is: 'target' = 2 * 'feature 0' - 1 * 'feature 1' + 1 * 'feature 2'. Based on the correlation between each feature and target, whether positive or negative, please guess the mean and standard deviation for a normal distribution prior for each feature. I need this for creating a linear regression model to predict the target. Provide your response as a JSON object with the feature names as keys, each containing a nested dictionary for the mean and standard deviation. A positive mean suggests positive correlation with the outcome, negative for negative correlation, and a smaller standard deviation indicates higher confidence. Only respond with JSON.
We use these rephrased task descriptions to elicit many Gaussian priors. We obtain a single Gaussian distribution for each feature, for each task description. By using a mixture of these distributions, we can construct the general prior knowledge of the language model on the features of a linear model.
Formally, given a language model \( M \) and task \( T \), we will obtain a single Gaussian prior for each feature, for each task description \( I \).
This is done by prompting the language model to provide a guess of the mean and standard deviation of a Gaussian prior for each feature on a linear model for a task description. From this we obtain a mean \( \mu_k \) and standard deviation \( \sigma_k \) for each feature, for a given task description \( I_k \).
By taking a mixture of these individual Gaussian distributions, we construct a prior \( \Pr_{M,T}(\theta) \) over our model parameters \( \theta \). With mixing weights for each task description \( \pi_k \sim Dir (1) \), this prior is given by: \[ \Pr_{M, T}(\theta) = \sum_{k=1}^K \pi_k N ( \theta | \mu_k, {\sigma_k}^2 ) \]
As an example, after combining the elicited distributions from synthetic task above, \( y = 2x_1 - x_2 + x_3 \), we arrive at the following prior distribution on a linear regressor:
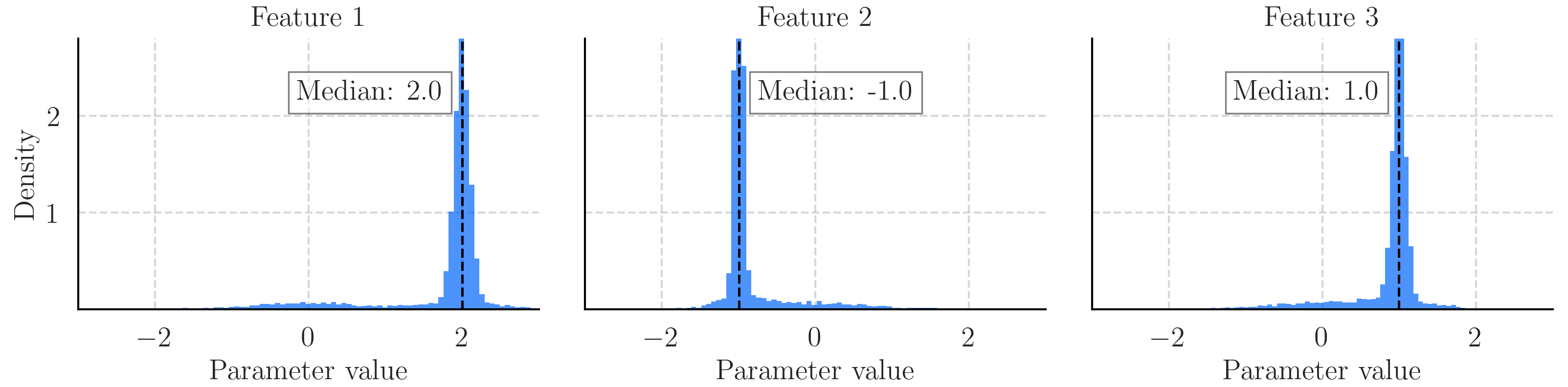
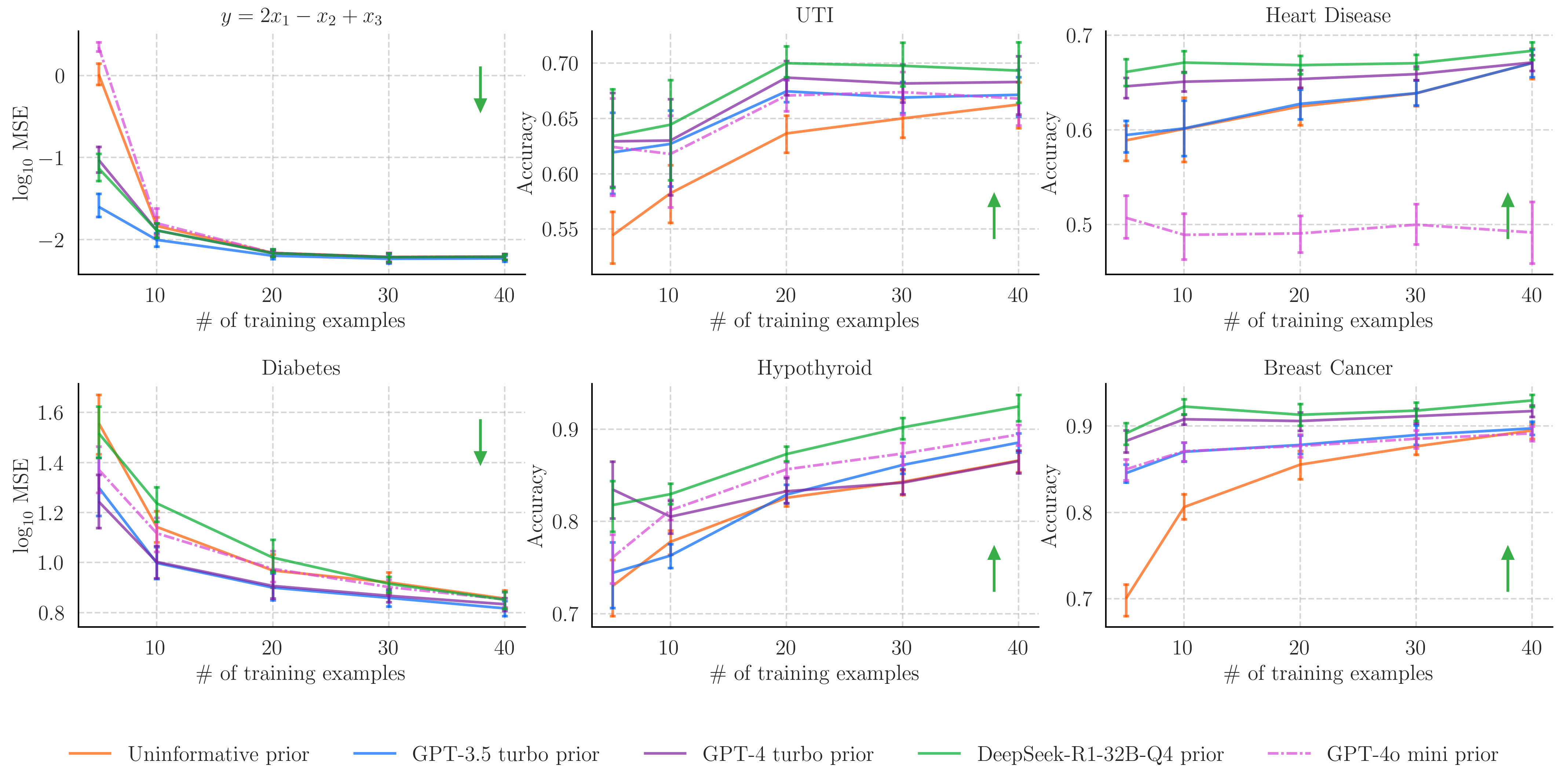
The elicited prior distribution is what we might expect, since we provided the LLM with the equation to produce the data. Along with this example, we also evaluate the language model's prior elicitation capabilities on a number of real-world tasks. We use Monte Carlo methods to sample the accuracy of the posterior predictive distribution on a test set after we have provided varied numbers of training examples (to the sampler, not the LLM). The uninformative prior in the below is a standard normal distribution.

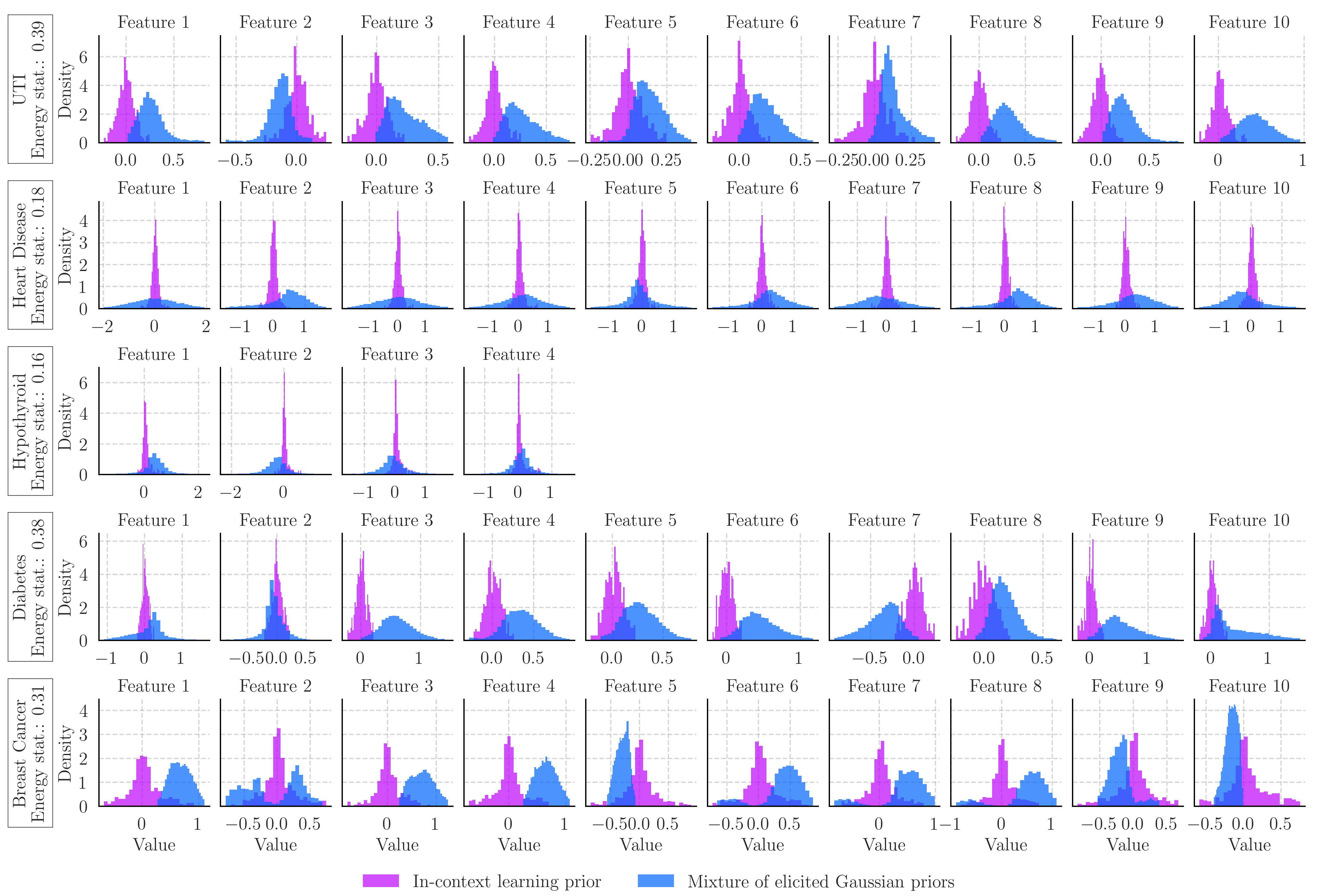
In almost all cases, one of the LLM-elicited priors outperforms the uninformative prior, particularly when data is sparse. This is particularly interesting for the UTI prediction task, where the data is private and will have never appeared in the LLM's training text.
For the Hypothyroid prediction task, the GPT-3.5-turbo-elicited prior performs similarly for the low-data regime but allows the model to learn more from the data as the number of examples increases. In this case, DeepSeek-R1-32B-Q4 produces considerably more accurate posteriors.
In the case of Heart Disease prediction, GPT-3.5-turbo returned an uninformative prior for most of the task descriptions, indicating its lack of knowledge of the domain. This suggests the use of human experts in communication with the LLM to help steer the language model towards producing more informative prior distributions when it has little prior knowledge.
By additionally providing the language model with expert knowledge, we can guide the LLM to return more informative priors. This can be helpful when practitioners have access to a domain expert, but it is challenging for them to define the parameters of a prior distribution.
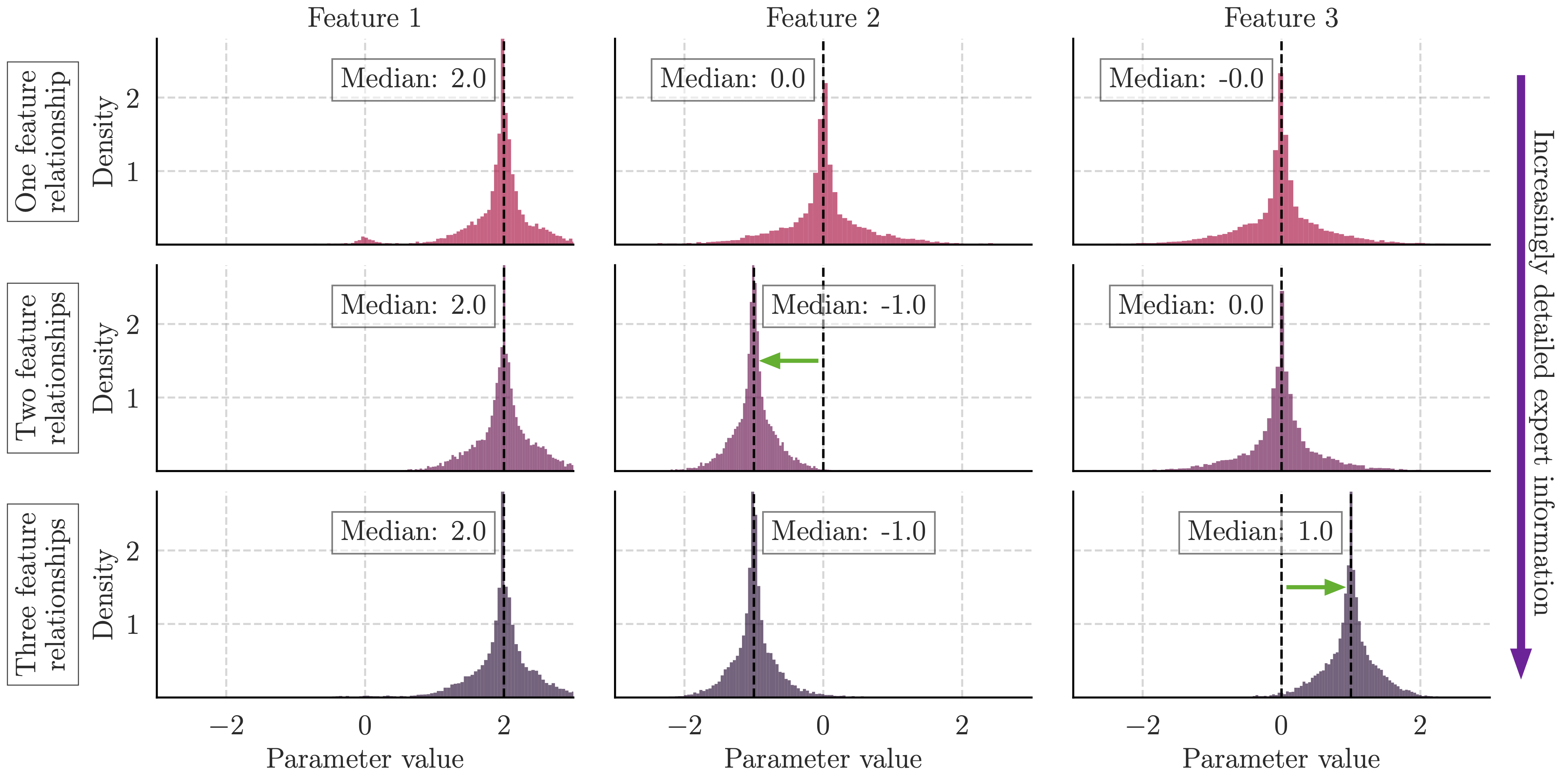
In the following figure, we use the synthetic task as an example. Here, we provide increasingly more informative information about the task to the language model and observe the expected changes in the elicited prior distribution. For each level of information, we describe to the language model how an additional feature relates to the target using natural language.
One feature relationship provided: The known relationship is: the target is a linear combination of the features and when 'feature 0' increases by 1, the target increases by 2.
Two feature relationships provided: The known relationship is: the target is a linear combination of the features and when 'feature 0' increases by 1, the target increases by 2, and when 'feature 1' increases by 1, the target decreases by 1.
Three feature relationships provided: The known relationship is: the target is a linear combination of the features and when 'feature 0' increases by 1, the target increases by 2, and when 'feature 1' increases by 1, the target decreases by 1, and when 'feature 2' increases by 1, the target increases by 1.
The same can be done on the UTI task, where we are able to provide additional information about the positive correlation between UTI risk and the bathroom frequency, night-time disturbances, and the number of previous UTIs.
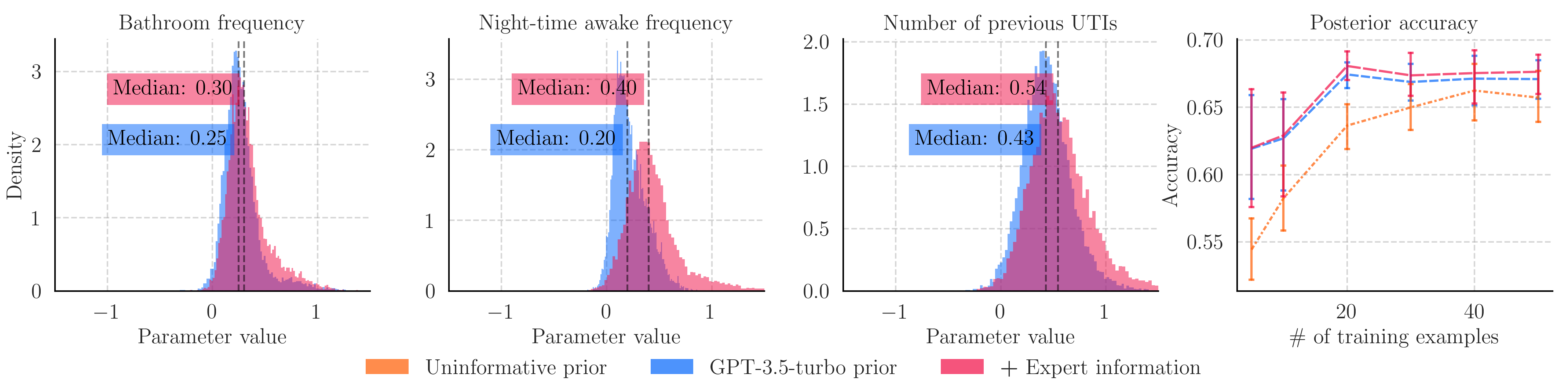
This figure shows how the language model updated its previously elicited prior distribution for the UTI task. As we can see, the LLM-elicited distributions already captured the correct correlation direction, but our additional information resulted in prior distributions with a greater value. Since the difference in prior distributions is small, this leads to only a small increase in the posterior accuracy. It does however demonstrate the combined use of experts and LLMs for prior elicitation, since the language model reliably converts the expert's natural language into prior distributions.
We can also evaluate the prior elicitation capabilities of other language models. Here, we compare open-source LLMs and some of the other available OpenAI models to those presented above:
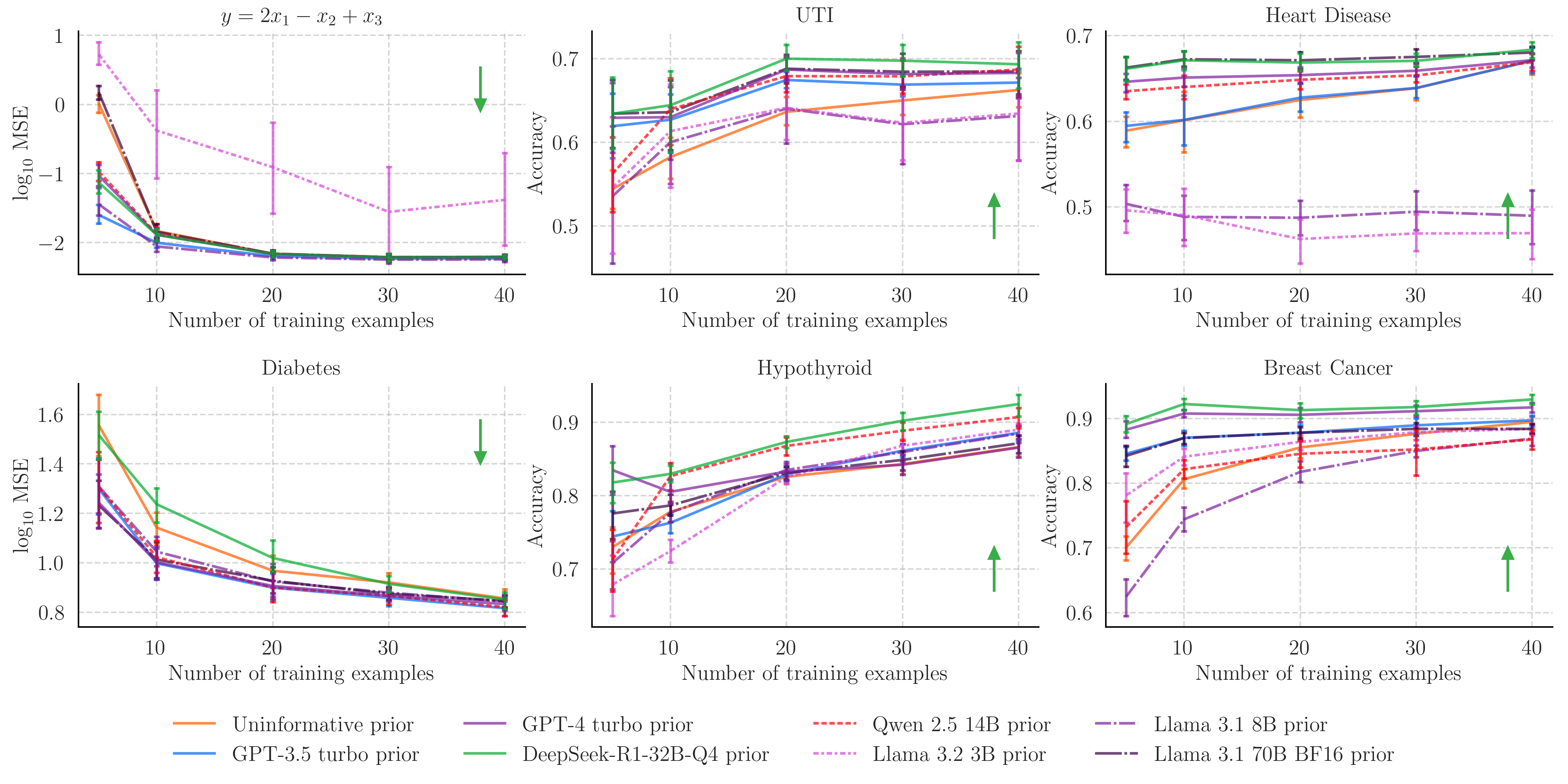
We mostly find that the open-source models provide priors with inconsistent posterior performance. The exception is DeepSeek-R1-32B-Q4, which suggests that recent developments in reasoning methods are helpful for eliciting priors.
Since we are using a language model's prior knowledge and updating it with a training dataset to make predictions, this method is a direct alternative to in-context learning for numerical predictive tasks. The difference being that prior elicitation uses a marginal distribution and Bayesian inference to address some of the shortfalls of in-context learning.
We present an approach for extracting the in-context prior distribution when the predictions mimic a linear model by sampling a maximum likelihood estimation (MLE) estimator. We construct a synthetic dataset, and given a task description, ask the language model to make predictions. We specify that the in-context predictions must be made using a linear model. If the language model has used a linear model to make its regression or classification probability predictions, we can use MLE to sample from the in-context model's prior and posterior distributions. From this we can construct sampling distributions of the parameters of the hidden in-context model.
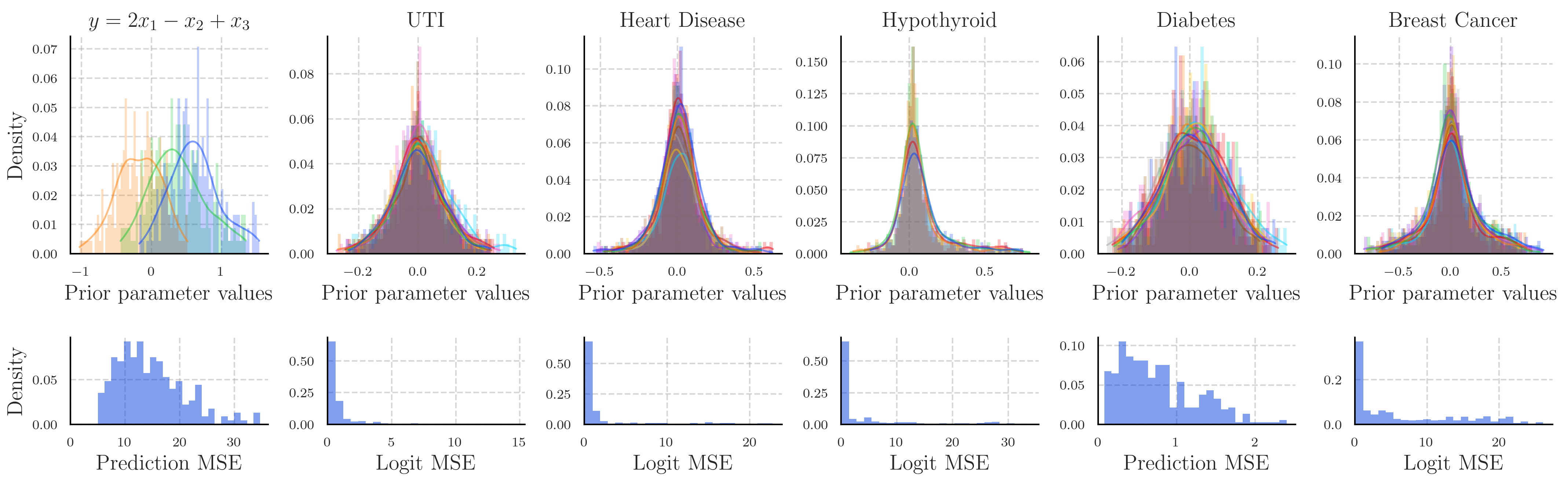
The approximated prior distributions for the in-context learning model are shown above. The upper row shows the histograms of parameters for each of the tasks, whilst the lower row shows the error in our approximations. We measure this by comparing the error in the predictions made using in-context learning and those made by the MLE approximations of the in-context model.
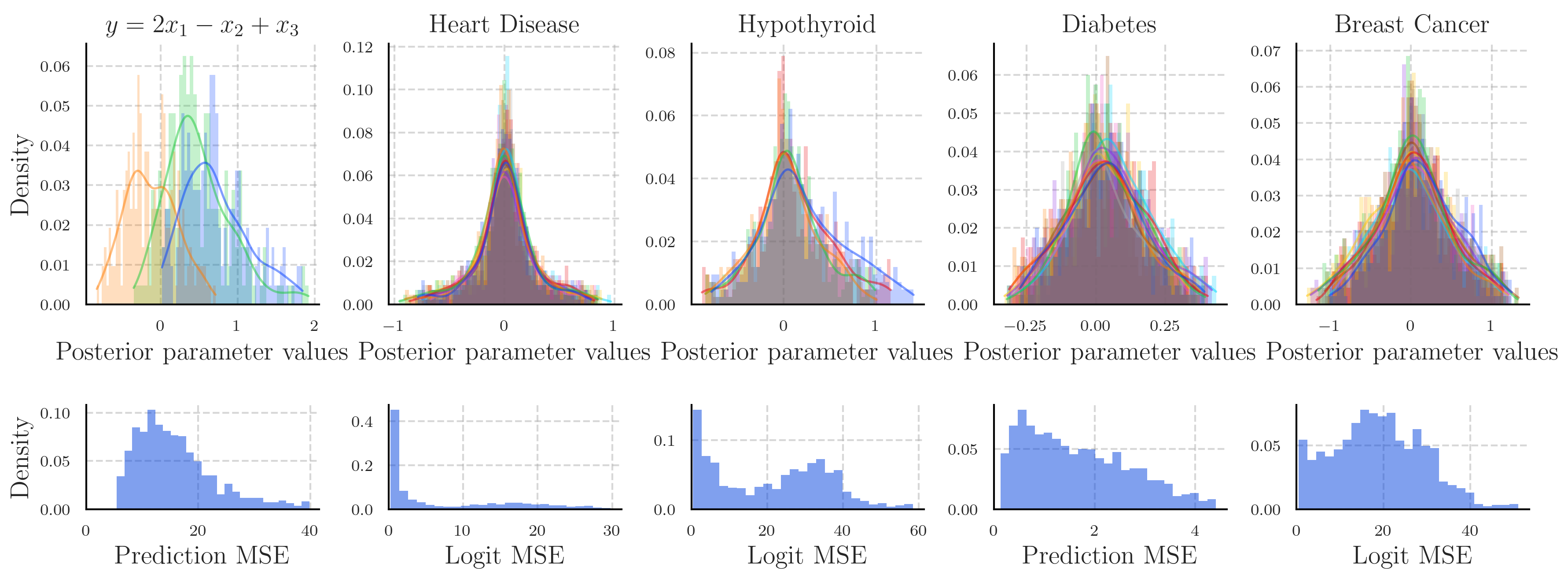
The above shows the posterior distributions approximated from the in-context predictions in the same way, except that the prompt also contains demonstration examples from the training data, which the in-context model should be using to update its prior knowledge.
We can see that our approximation of the internal posterior model is not as accurate as the internal prior model. This is because the LLM is inconsistently imitating a linear model as we instructed, likely because the prompt significantly increases in size once we include data points as examples.
In the figure below we can then compare visually, and using the energy statistic, the difference between the approximated in-context prior distributions and the ones elicited from the language model. Discounting the synthetic task which shows a high error in our approximation, we see that the distributions elicited from the LLM differ significantly from those used by the language model in-context. Either the language model is not reliably returning its own priors when we perform prior elicitation, or it is not using that prior knowledge when making predictions in-context. We suspect the latter, since the elicited priors match our expectation on the UTI and synthetic tasks, and the in-context priors often centre around 0.
Since we can also approximate the in-context model's posterior distribution by providing training examples in the prompt, we can evaluate to what extent the in-context model is approximating Bayesian inference. By applying Monte Carlo techniques to the approximated in-context prior, we can sample a posterior distribution that should match the one we approximate using MLE sampling of the in-context predictions.
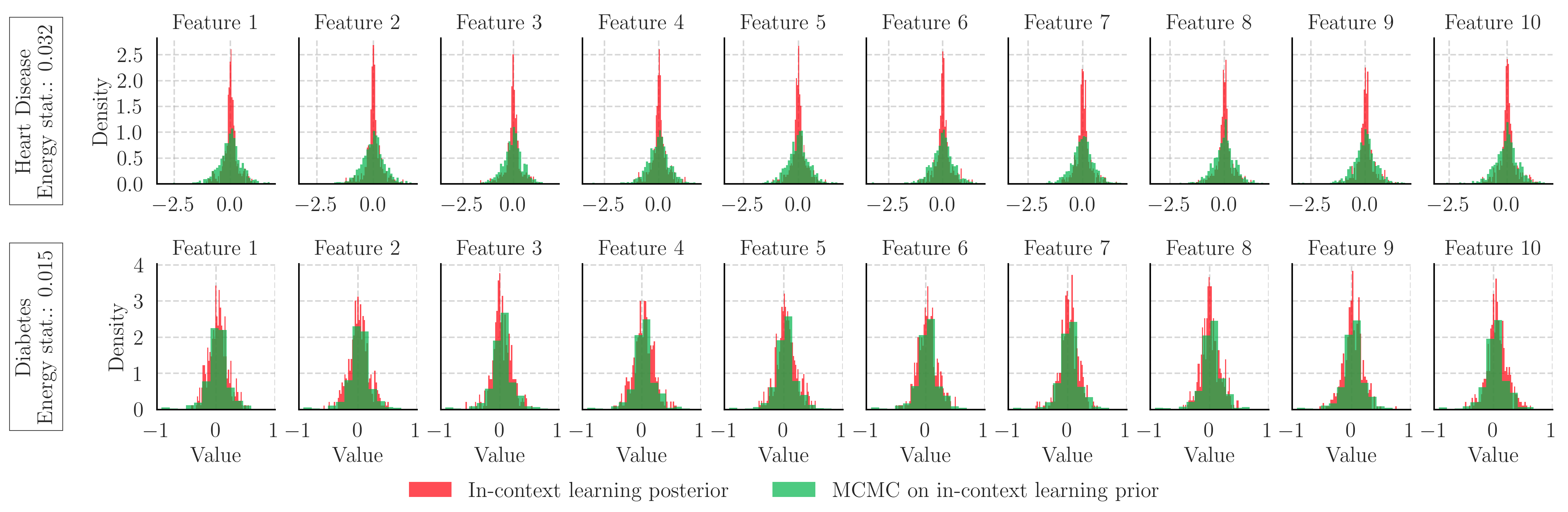
The above figure shows these two distributions, that should match if our approximations are good and if the LLM is performing Bayesian inference in-context.
Since we make an in-accurate approximation of the posterior distribution for the Breast Cancer and Hypothyroid prediction tasks, we will ignore it. However, for the other tasks our approximations for the prior and posterior in-context distributions have low error.
In the case of Heart Disease prediction, the difference in the posterior distributions estimated through MLE sampling and using Monte Carlo methods differ significantly suggesting that the LLM is not approximating Bayesian inference for this task. On the other hand, for the Diabetes predictive task, both distributions are more similar, signifying that in this case the language model is performing Bayesian inference in-context.
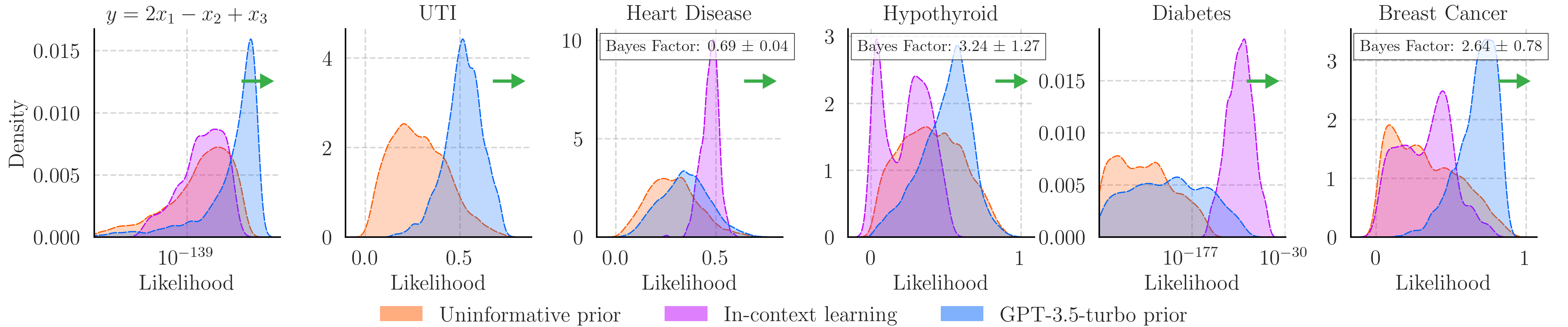
We can also calculate the Bayes factor between the prior elicitation predictions and those made using in-context learning. The figures show the prior accuracy and MSE as well as the prior likelihood on 25 data points from each task. Whether prior elicitation or in-context learning provides greater likelihoods depends on the task, with both methods being the better choice over a non-informative prior for all cases tested. When factoring in the methods' abilities to estimate Bayesian inference and the cost of producing predictions however, prior elicitation is likely the better option for the cases tested.
Performing prior elicitation using language models proves to be an effective technique to improve probabilistic model performance in the low data regime.
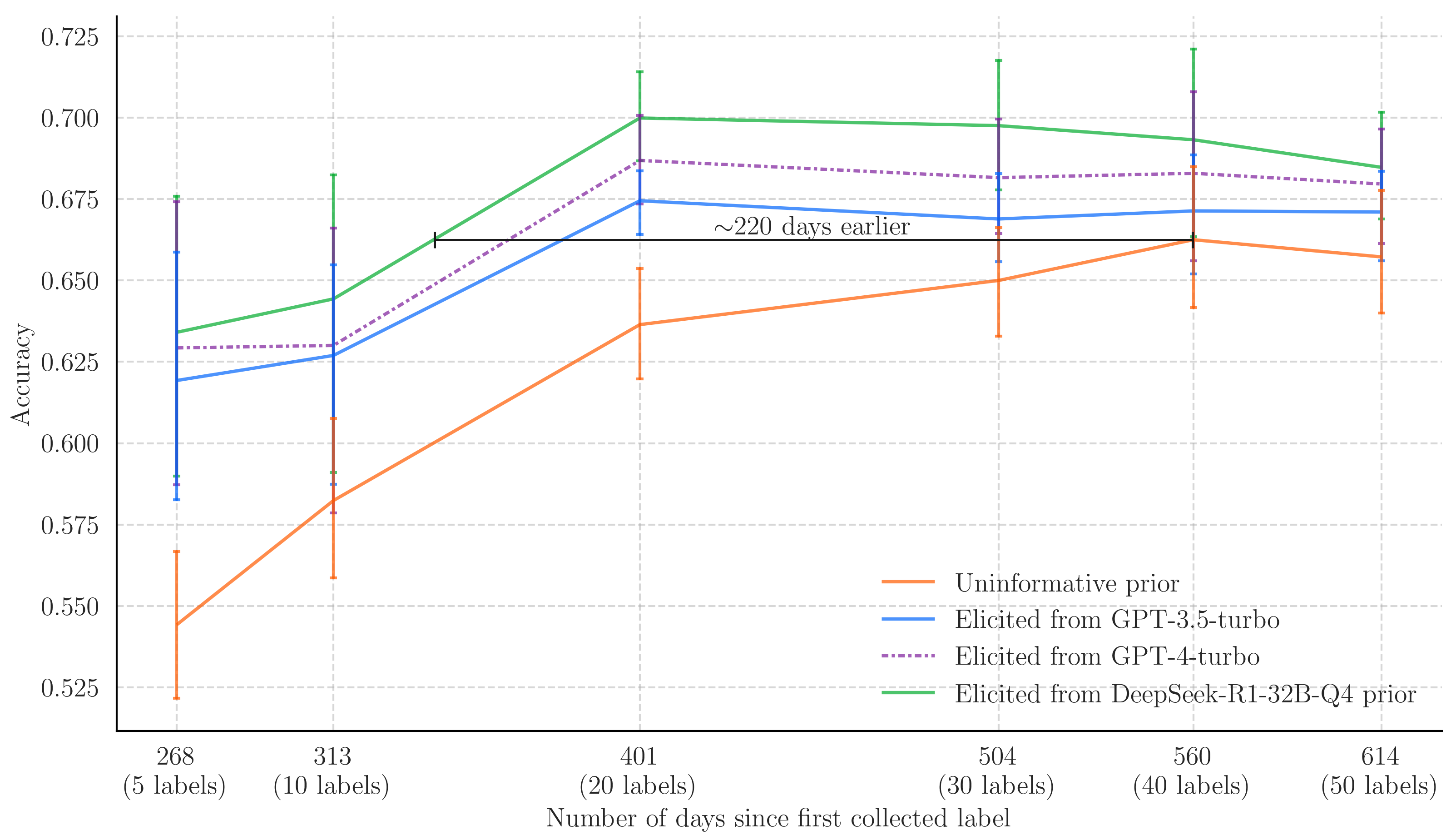
In the figure above we plot the length of time it took to collect a given number of labels against the accuracy of a model using an uninformative prior and one elicited from a language model. This result illustrates the usefulness of prior elicitation, since we can achieve comparable (and ultimately better) accuracy with less data points, and therefore less data collection time.
@article{capstick2024autoelicit,
title={AutoElicit: AutoElicit: Using Large Language Models for Expert Prior Elicitation in Predictive Modelling},
author={Capstick, Alexander and Krishnan, Rahul G and Barnaghi, Payam},
journal={arXiv preprint arXiv:2411.17284},
year={2024}
}